In the late 1800’s, physics was facing a crisis. Physicists were trying to model the energy of an atomic orbital. All the physics they knew at that point said it should look a certain way, but reality looked completely different and no one knew why.
The solution was found by Max Planck. Previously physicists had assumed the microscopic world of an atom’s energy was continuous; that is, the energy of each electron orbital should be able to take on any value. However, Planck correctly assumed that they could only have the energies that were whole number multiples of some base frequency, which he called “h”. In other words, in the microscopic world of atoms energy appears to be quantized in a manner that corresponded to a whole number of the frequency “h” or Plank’s constant.
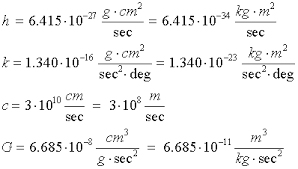 |
However, Einstein, in his General Theory of Relativity defined energy in the macroscopic environment of stars and planets in terms of the continuous field properties of space-time. T
he problem now became how can one integrate the continuous field properties of energy as described by Einstein with the discontinuous properties of an atomic orbital associated with Planck’s constant.
In the past most researchers have attempted to do this without success by attempting to define its continuous field properties in terms of the discontinuous quantum properties associated with Planck’s constant.
However, one may be able to if, instead of attempting to the define those properties in terms of discontinuous properties associated with an atomic orbital, we attempt to derive the discontinuous or quantum properties of an atomic orbital in terms of the continuous field properties of space-time.
One of the difficulties in visualizing and understanding how this would be possible may be because Planck’s constant is defined in terms of the spatial not the time components of a system while Einstein’s theories define energy in terms of time or a space-time dimension.
However, Einstein gave us a way to make it easier when he qualitatively and quantitatively derived the geometric properties of his space-time environment in terms of the constant velocity of light and the velocity of objects that do not move at that speed because it allows one to redefine a unit of time he associated with energy in his space-time universe to its equivalent unit of space in a universe consisting of only four *spatial* dimensions.
In other words, by defining the geometric properties of a space-time universe in terms of the constant velocity of light he provided a qualitative and quantitative means of redefining the geometry pf his space-time universe in terms of its equivalent in four *spatial* dimensions.
The fact that one can use Einstein’s equations to qualitatively and quantitatively to redefine the displacement in space-time he associated with energy in terms of its equivalent in four *spatial* dimensions is one bases for assuming as was done in the article “Defining energy?†Nov 27, 2007 that all forms of energy in including that of an electron orbiting the nucleus can be derived in terms of a spatial displacement in a “surface” of a three-dimensional space manifold with respect to a fourth *spatial* dimension as well as on in four dimensional space-time.
For example as the article “Why is energy/mass quantized?” Oct. 4 2007 showed one could derive a model for an atomic orbital by extrapolating the laws of a resonance in our three-dimensional spatial environment to one made up of four.
Briefly, it showed the four conditions required for resonance to occur in a classical environment, an object, or substance with a natural frequency, a forcing function at the same frequency as the natural frequency, the lack of a damping frequency and the ability for the substance to oscillate spatial would be meet by a matter wave in four *spatial* dimensions.
The existence of four *spatial* dimensions would give space (the substance) the ability to oscillate spatially on a “surface” between a third and fourth *spatial* dimensions thereby fulfilling one of the requirements for classical resonance to occur.
These oscillations would be caused by an event such as the decay of a subatomic particle or the shifting of an electron in an atomic orbital. This would force the “surface” of a three-dimensional space to oscillate with the frequency associated with the energy of that event.
However, these oscillations in a continuous non-quantized field of energy caused by such an event would result in a resonant system or “structure” to be formed in space.
Classical mechanics tells us the energy of a stable resonant system can only take on the discreet quantized values associated with its resonant or a harmonic of its resonant frequency.
In other words, value of Planck’s constant can be understood by assuming that it defines the energy of the fundamental resonate frequency of field properties of space-time as defined by Einstein and therefore, the energies all orbits must be multiples of that fundamental frequency.
However, one can also use the above theoretical model to explain the why quantum properties of Planck’s constant must be applied to all stable particles including photons.
In classical physics, a point on the two-dimensional surface of paper is confined to that surface. However, that surface can oscillate up or down with respect to three-dimensional space.
Therefore, an energy wave, occupying a volume of three-dimensional space would be confined to it. similar to the surface of the paper when it is forced to oscillate “\”up” or “down” with respect to a fourth *spatial* dimension.
The confinement of the “upward” and “downward” oscillations of a three-dimension volume with respect to a fourth *spatial* dimension by an observation is what defines the spatial boundaries associated with all particles including photons in the article “Why is energy/mass quantized?”.
Not only that but it can be shown these resonant systems in a continuous field properties of space-time that are responsible for the incremental energies associated with an atomic orbital and Planck’s constant are also responsible for the energy profiles of black body radiation.
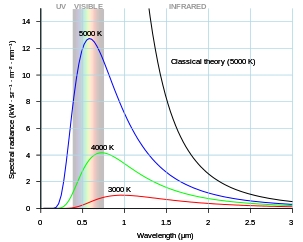 |
| The ultraviolet catastrophe is the error at short wavelengths in the Rayleigh–Jeans law (depicted as “classical theory” in the graph) for the energy emitted by an ideal black-body. The error, much more pronounced for short wavelengths, is the difference between the black curve (the wrong curve predicted by the Rayleigh–Jeans law) and the blue curve (the correct curve predicted by Planck’s law). |
At room temperature, black bodies emit mostly infrared wavelengths, but as the temperature increases past a few hundred degrees Celsius, black bodies start to emit visible wavelengths, appearing red, orange, yellow, white, and blue with increasing temperature. By the time an object is white, it is emitting substantial ultraviolet radiation.
The problem is the laws of classical mechanics, specifically the equipartition theorem, states that black-bodies which have achieved thermodynamic equilibrium are mathematically obligated (by classical, pre-quantum, laws) to radiate energy in the form of ultraviolet light, gamma rays and x-rays at a certain level, depending on the frequency of emitted light.
However, observations of black body radiation indicate that there was less and less energy given off at high end of the spectrum.
Einstein pointed out this difficulty could be avoided by making use of a hypothesis put forward five years earlier by Max Planck. He had hypothesized that electromagnetic energy did not follow classical laws, but could only oscillate or be emitted only in discrete packets of energy proportional to the frequency, as given by Planck’s constant. In other words, the light waves of each frequency in a black body could not have any energy but are limited to a few discrete values.
However, as mentioned earlier the article “Why is energy/mass quantized?” showed energy of a photon at each frequency could be understood by extrapolating a physical image of a resonant system in three-dimensional space to a fourth *spatial* dimension similar to how Einstein was able to from a physical image of gravity.
For example, as the above theoretical model shows using only the concepts of classical physics and field properties of Einstein’s Theory of Relativity a photon could only have the discrete energies or frequencies that are a fundamental or harmonic of the energy of an environment which would be determined by the temperature of the one it was occupying. Therefore, according to the above theoretical model any frequency other than that would be irregular and non-repeating and would be absorbed into the fundamental or harmonic frequency of that environment.
In other words, it explains in terms of a physical image based on our classical reality why black-bodies which have achieved thermodynamic equilibrium are mathematically obligated by to radiate energy in the form of ultraviolet light, gamma rays and x-rays at certain discrete levels, depending on the frequency of emitted light because of the field properties of Einstein space-time universe.
As was shown above one can use the resonate field properties of a space-time environment to explain why the energy of a black body is what it is and why all particles AND the electrons orbiting in atoms can only have the energies that are a whole number multiples of the energy associated with Planck’s constant “h”. 
It should be remembered; Einstein’s genius allows us to choose if we want to view the physical properties of Planck’s constant in either a space-time environment or one consisting of four *spatial* dimension when he defined the geometry of space-time in terms of the constant velocity of light. This interchangeability broadens the environment encompassed by his theories by making them applicable to both the particle and wave properties microscopic quantum world as well as microscopic one of Einstein thereby giving us a new perspective on the physical relationship between particles and waves.
Later Jeff
Copyright Jeffrey O’Callaghan 2019
Please visit our Facebook group The Road to unification of Quantum and Relativistic theories if you would like to comment or contribute to our project
The Road to Unifying | The Road to Unifying | The Road to Unifying |


